当前位置: 主页 > 资讯中心 > 公司新闻 » 柯西,积分第一,积分第二中值定理的物理或几何意义
这里不作任何铺垫,默认你有微积分基础
柯西中值定理:设函数 在
上连续且在
上可微,则存在一个点
使得
若 ,则还可以变形为
我们记,在 平面内沿一光滑曲线运动的点
在
时的坐标为
,其中
,曲线的起点和终点分别是
则 在
时的速度向量
为
,起点到终点的位移向量
为
可以找到曲线上的一点 ,使得
在该点的速度向量
的方向与位移向量
的方向一致
如图1
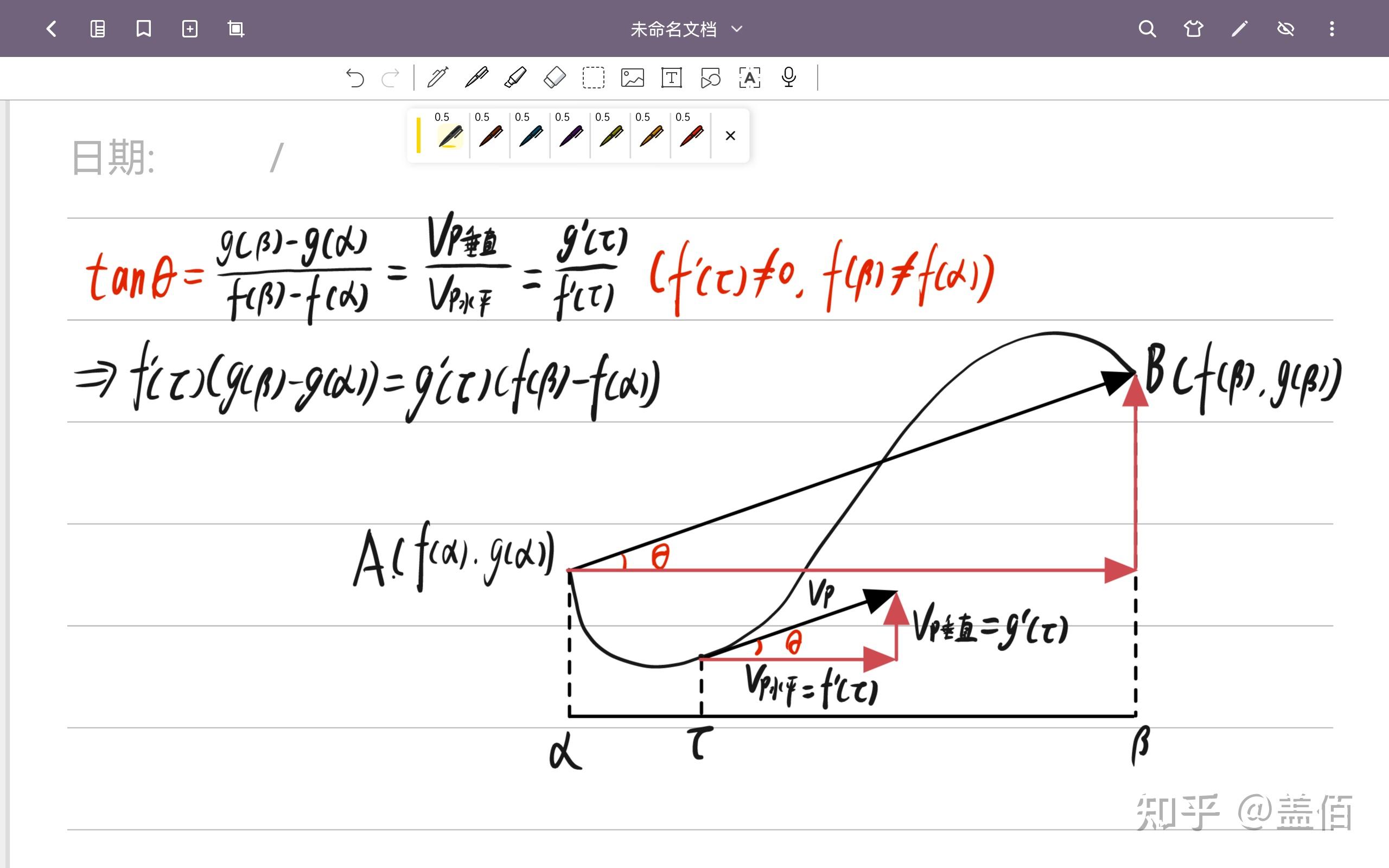
本应该是 的三维图,但画起来好复杂,简化了一下,下方的
线段是
到
的时间间隔
积分第一中值定理: 令 ,且
,若
在
上非负(非正同理),则
为了解释上面定理的几何意义,我们先讨论一个简单的情形,令
有朋友应该已经想到了如图2的几何意义
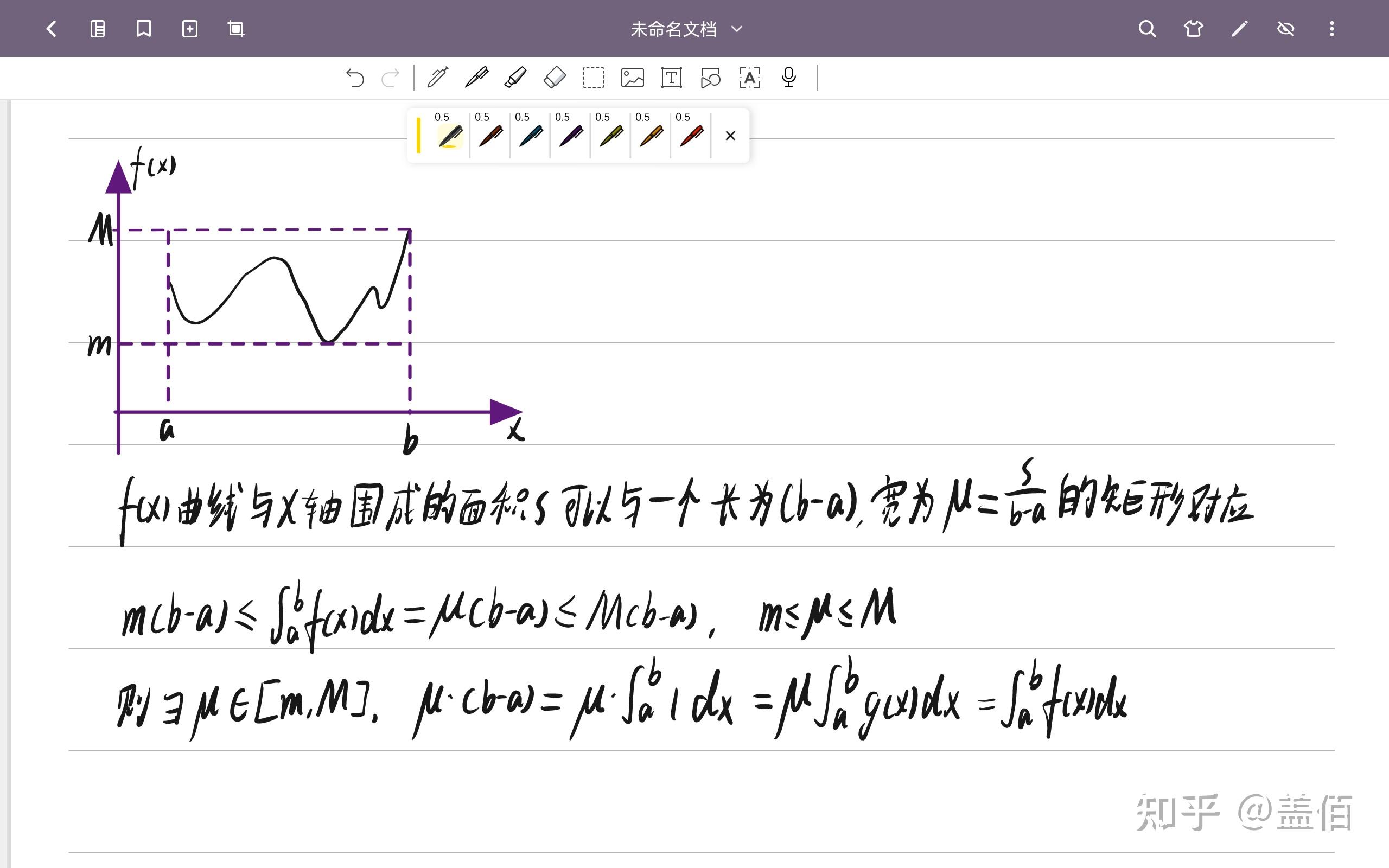
思路是对的,但并不利于解释完整的定理
我们把平面直角坐标系换成空间直角坐标系, 的图像分别在
平面上,于是根据我们之前所假设的情形,有图3
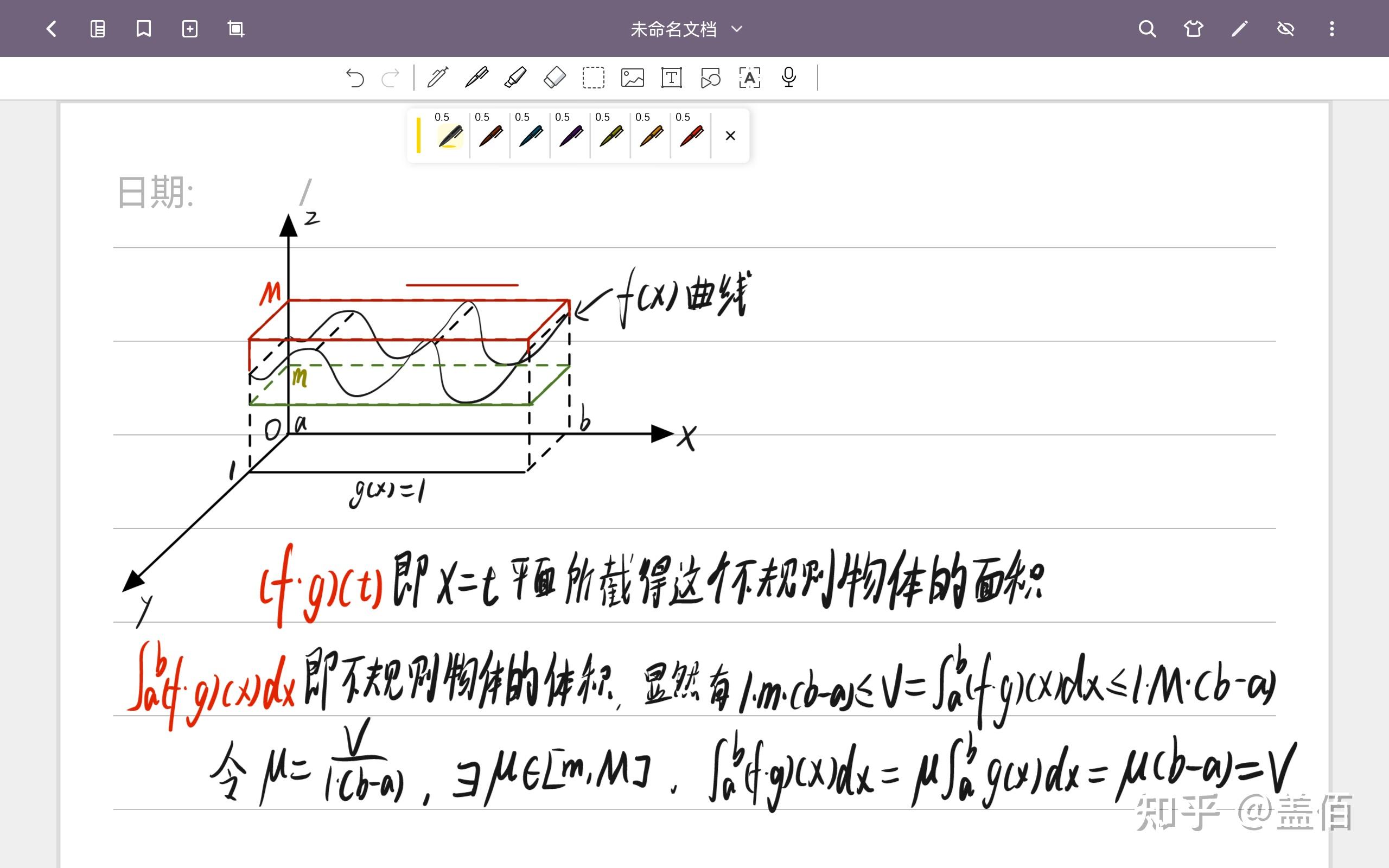
最简单情况下,积分第一中值定理的几何意义已经凸显了,接下来弱化限制,令 ,于是有图4,
同理
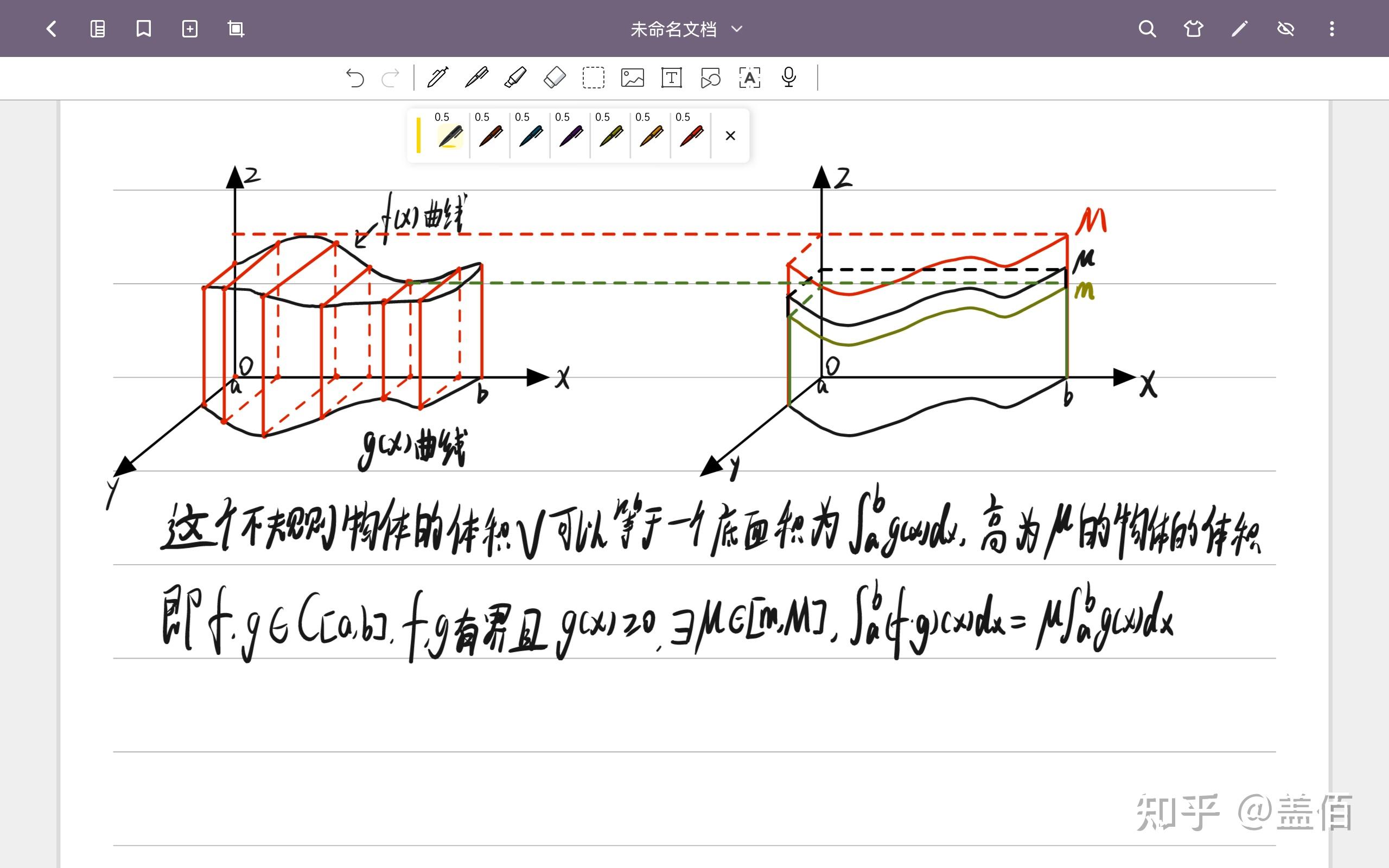
但定理仅要求 ,因此函数
在
有界且可能存在有限个间断点
为了处理这种情况,给出以下定义、命题与引理,命题与引理不作证明
是给定的函数,若
,则记
若
,则
若
,则
,且有
设
是有限或无限区间,
是定义在该区间上的函数,且
,若
时,
存在,则定义
若
,则常义积分
与反常积分
的值是一样的
有了上述结论,对 在
上各自的间断点集取并,得到有限可数集
,
进而根据 ,
在
和每个形如
的小闭区间上都是可积的,且在对应的小开区间上都是连续的,有
最后再根据 ,原积分的值
就会等于每个小开区间上有界连续函数
的反常积分的值的总和
于是,对于 出现间断点的情况,可以把
划分为
和所有形如
的开区间,
在每个小开区间上都是连续且有界的,进而在每个小开区间上可以继续用图4所示的几何意义来解释,
时同理
积分第二中值定理:令 ,且
在
上单调,则
依旧从简单情形开始,令 ,但此时有
,没有啥特别的,于是我们令
,有图5
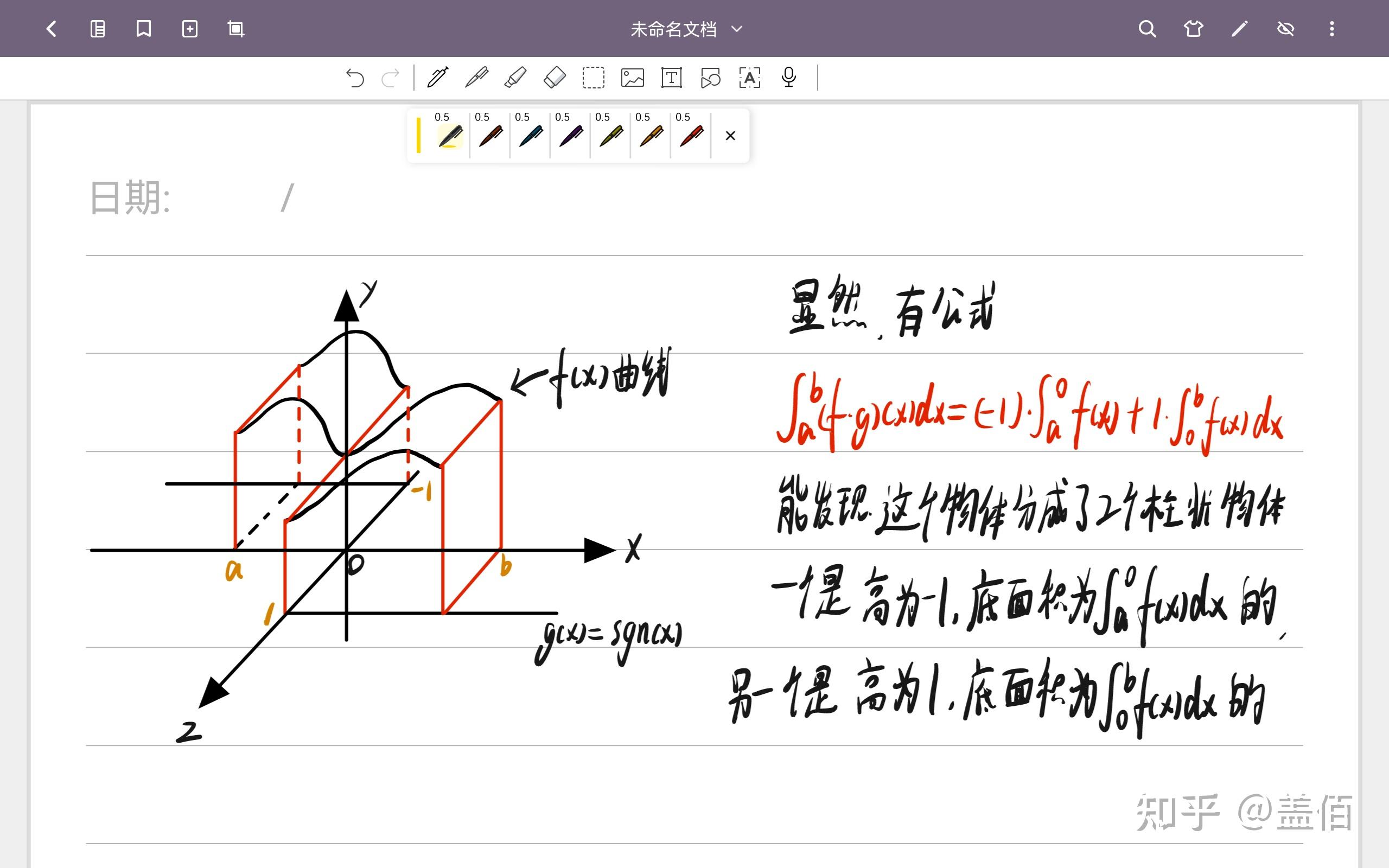
接下来弱化限制, ,
在
单调,则有图6
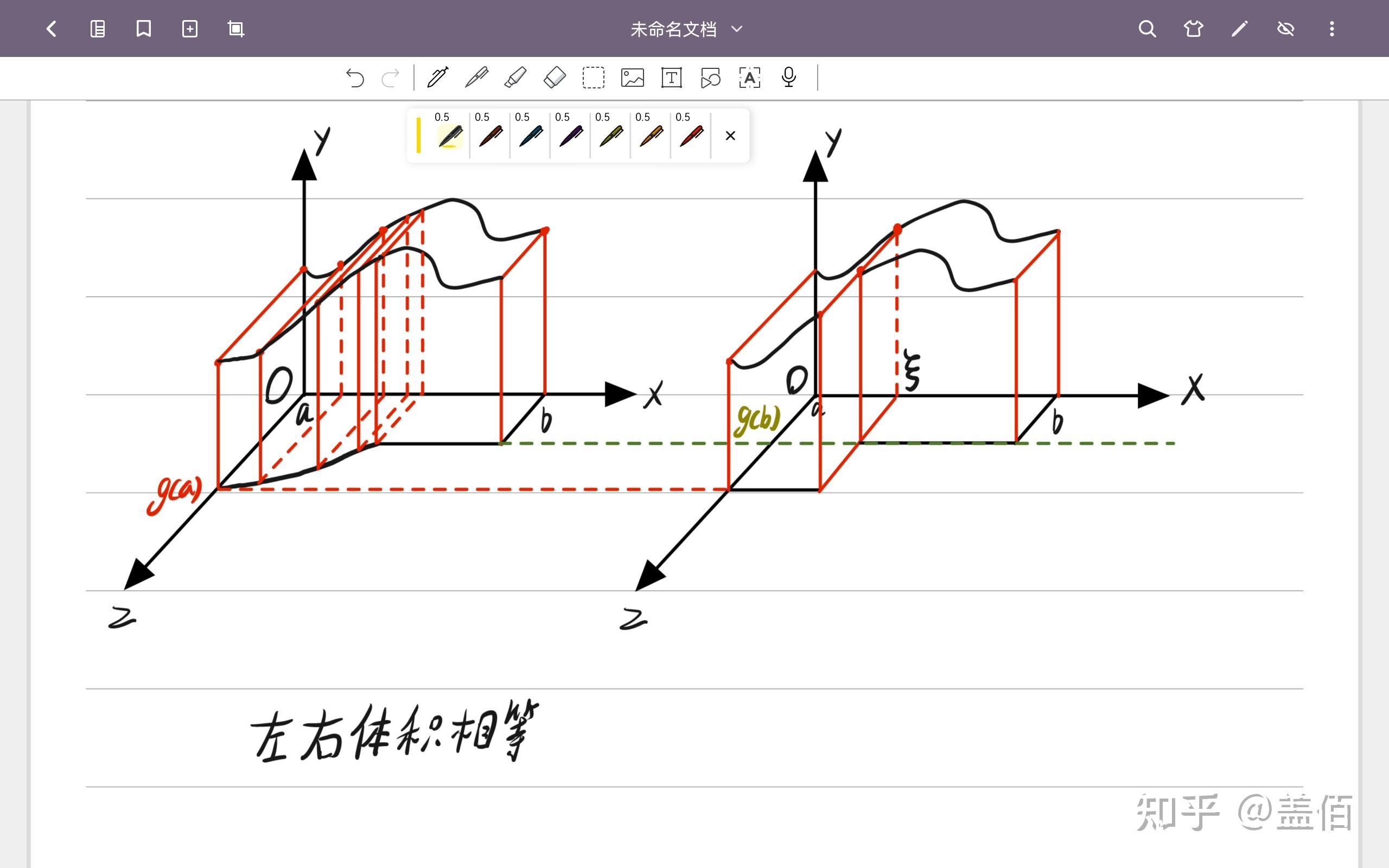
而定理的完整条件是令 ,且
在
上单调,则
有界且也有可能出现有限个间断点,处理方式与解释积分第一中值定理时类似
欢迎指出错误与提出意见
